The original paper can be found here and the associated repository can be found here.
Introduction
In 2022, the value of the NYC housing market was estimated at $3.51 trillion, and it appears that the market is not expected to stop growing anytime soon. The idea that real estate is a wise investment is a heavily debated topic, especially as young people grow more and more hesitant towards making such a purchase; but if one is to make it, it should be a wise one that functions more like an investment.
New York City has been publishing large sets of property data on the internet since 2003. Online, the Annualized Sales Updates feature all sales since 2003, broken down by detail and by borough; furthermore, their website also features Rolling Sales Data, which features sales from the past 12 months. Property Valuation and Assessment Data can provide data on properties that haven’t been sold in the past 20 years.
While it is widely known that the highest price per square foot can be found in Manhattan, I’d like to discover the value added exclusively by nature of a property being featured in a given borough, accounting for the most notable luxuries and pitfalls of living in a given area. Those qualities include but are not limited to: the quality of the transportation in area, the square footage of apartments in the borough, and the median income level of the surrounding area.
The population data by zip code was gathered from data.betaNYC , income and demographic data was gathered from The U.S. Census Bureau , and the sales data is from NYC OpenData for the year 2021. Now the question is regarding where to buy: which location provides the most bang for your buck? In which of the boroughs would one be paying the most for exclusively the right to admit to living in a given borough? That will be my treatment variable. I hypothesize that Manhattan is the most overrated, and will result in the price of having a place in Manhattan (and only the value of being able to claim a location in Manhattan) being the highest.
Preliminaries
Causality
A directed acyclic graph is a series of nodes connected by directed edges, which can be articulated as a touple consisting of the vertices and their connecting edges with independent errors equipped with the do-operator . Such a graph cannot contain a cycle. A causal model of a such a graph where each variable is considered a function of its parents and the independent error term, so the probability of a given variable V which can factorize via the following formula, where pa𝒢(Vi) represents the parents of a variable Vi in 𝒢:
$$\begin{aligned}
p(V) = \prod_{V_i \in V} p(V_i | \operatorname{pa}_{\mathcal{G}}(V_i)),\end{aligned}$$
where pa𝒢(Vi) is the parents of Vi in 𝒢. Within the context of the causal model, pa𝒢(Vi)→Vi can be understood as pa𝒢(Vi) is the direct cause of Vi.
ACE & Backdoor Adjustment
The aim of this paper will be to find the average causal effect (ACE) of a variable a on an outcome Y; ACE is most efficiently defined as the difference between the expected value of the outcome when the variable is present versus when it is not. There are multiple methods of finding the ACE, including (augmented) inverse probability weighting, instrumental variables, or front-door adjustment. None of these other methods were used because backdoor adjustment efficiently blocks spurious correlations; given the number of variables included in this experiment, and their plausible interconnections, this is essential in order to maintain faithfulness.
Backdoor adjustment requires a valid set that blocks any paths from the treatment to the variable, ignoring the directionality of the edges. This set allows for the following formula to be true and provides the average causal effect according to backdoor adjustment criterion:
∑Zp(Z)×𝔼[Y ∣ A = a, Z]
Which can be articulated as the average difference between the expected value of the outcome variable given that it is set to 1 versus when it is set to 0. The formula is used in backdoor.py, where n is the number of entries, Y is the outcome variable, and a is the treatment when it is set to 1, and a′ is the treatment when it is set to 0.
$$\hat{ACE} = \frac{1}{n}\sum_{i=1}^n (\hat{Y_i(a)}-\hat{Y_i(a')})$$
Conditional independences in p(V) can be read off from the DAG via d-separation, i.e., (X ⫫ Y | Z)d-sep ⇒ (X ⫫ Y | Z)in p(V). This can be used in order to find a valid backdoor adjustment set; however, this requires the creation of and valid use of a DAG, as described above.
While backdoor adjustment does prevent the emphasises towards spurious correlation, the one major issue with it is the associated linearity assumption: this may yield inaccurate conclusions regarding the relationship between variables created by the model.
Bootstrapping
In order to create a slightly more robust result for a limited data set, a method called bootstrapping may be used: it is a technique where a data set is sampled in order to manufacture more data, having calculated the corresponding probabilities. In the context of this paper, random resampling will be used in order to increase the quantity of data points featured in the calculation of the backdoor adjustment-based ACE.
Tetrad
A tool for causal discovery that I will be using in order to find a directed acyclic graph that I could use in order to test the relationship between my treatment variables and the sale price of the properties on average. Given that my data is not from a randomized control set, Greedy Equivalence Search (GES) will be run on my data in order to find possible causal structures in my data. GES is a score-based method for learning DAGs , assuming that there are no unmeasured confounders in my data. This seems to be a vaguely reasonable assumption given the quantity of different variables included in my data set. The particular version used in Tetrad is the Fast Greedy Equivalence Search (FGES), which is optimized for parallel processing, allowing for the computations to be much faster for the 31,488 entries that I have in my data set, as described in .
FCIT
The Fast Conditional Independence Test is a nonparametric conditional independence test, good for testing the presence of edges between two variables: when the result is higher than a given alpha value, then the presence of the edge is questionable. It bases its approach on that when P(X | Y, Z) does not equal P(X | Y ), including Z can improve predictions. Instead of assuming a linear assumption, this is the assumption they make regarding their predictions. The process uses a decision tree regression to predict an outcome under two different circumstances: one where only the some non-treatment variable is given and one where the treatment and the non-treatment variable are given. It then returns a p-value that compares the accuracy of the relationship in the context of the data, versus the null hypothesis. This, unlike FGES and normal backdoor adjustment is not linear.
Methods
Data Collection
My primary source for the property sales from the past 12 months in New York City can be found in from . However, this inspired further inquiries regarding the area, not only the properties and residences themselves: this paper is focusing in the role of the name, not necessarily the traits. Therefore, I started to gather data from multiple different sources, and ended up with a conglomeration of five different courses for my data sets. The quantity of subways was found in , the population densities by zip code were found on , and the average income for a given area was found in , and the racial demographics were found in . Given that there are multiple different ways of politically dividing the regions of the location (neighborhood, borough, block, zip code), I wanted to have a degree of specificity that would encompass all of the variety present in a given borough (which is the treatment variable of this experiment), but was still reasonable and accessible and wouldn’t introduce excessive variance in the data. The U.S. Census Bureau features robust filters on their website, and using that feature, I was able to categorize the average income and racial demographics by zip code and use that for processing.
Data Pre-processing and Cleaning
Because this data is not collected from a randomized control trial, backdoor adjustment is a reasonable option to be used to adjust for confounding variables. My data was cleaned and organized in such a way so that for each given property collected from the 2021 New York City Sales Data, there were corresponding properties, based off the zip-code of the address listed with the property. After all of the data was processed, the listed variables were included for each of the properties:
SALE_PRICE: The price a given property was sold at.
ELEVATOR: A binary variable marking presence of an elevator in the property.
RESIDENTIAL_UNITS: The number of residential units in the property.
COMMERCIAL_UNITS: The number of commercial units in the property.
LAND_SQUARE_FEET: The number of square feet on the property.
SERVICES_COUNT: The number of subway lines that run through the subway stops in the neighborhood.
COOP: Binary variable describing whether or not the property is in a co-op.
CONDO: Binary variable describing whether or not the property is a condo.
FAMILY_DWELLING: Binary variable describing whether or not the property is a house, rather than an apartment.
MEDIAN_INCOME: The estimated median income in the property’s zip code.
POPULATION_DENSITY: The population density of the property’s zip code.
PERCENT_WHITE: The percent of white people in the property’s zip code.
STATEN_ISLAND: Binary variable indicating whether or not the location is in Staten Island.
BRONX: Binary variable indicating whether or not the location is located in the Bronx.
MANHATTAN: Binary variable indicating whether or not the location is located in Manhattan.
QUEENS: Binary variable indicating whether or not the location is located in Queens.
BROOKLYN: Binary variable indicating whether or not the location is located in Brooklyn.
Graph Elicitation
Regarding the parameters in Tetrad, the maximum degree of the graph was assigned to be 10 because of the already high quantity of variables involved with this data set. The algorithm was parallelized in order to improve processing times even further, and in order to increase the robustness of the algorithm, 20 bootstraps were featured.
Considering the binary nature of my treatment variables, I will be able to run backdoor adjustment on my DAG (which has been generated from Tetrad) in order to find the ACE of the property being in a given borough on the cost of the property.
I will be featuring 5 treatment variables, which all affect one another directly: BRONX, BROOKLYN, MANHATTAN, STATEN_ISLAND, and QUEENS. Only one of these variables could be set to true at any one given time because a real estate property can only be in one given borough at any one time, and therefore should be a direct causal relationship between all of these variables– by being in Brooklyn, you are therefore in no other boroughs.
Causal Discovery
As described in section ACE & Backdoor Adjustment, I will use backdoor adjustment in order to calculate the relationship between my treatment and outcome variable. The code for backdoor adjustment was written up in Python3 and featured heavy use of statsmodels.api} in order to calculate a Gaussian model for the relationship between my treatment variables and the outcome. The code for this is featured in backdoor.py, in the function backdoor_adjustment. In order to compute the corresponding confidence intervals, 200 bootstraps were features in the compute_confidence_intervals_backdoor function, with an alpha value of 0.05 in order to assess the variability of the distribution of results found from the backdoor adjustment processing. This process was run in a for loop for each my treatment variables, adjusting the adjustment set as needed.
Results
Having run a Greedy Equivalence Search in Tetrad, the graph featured in Figure 1 was found. This graph, while complex, can be used to find the backdoor adjustment set by grabbing all of the parents of the outcome variable, with the exception of the treatment variable being tested, whether it be BRONX, BROOKLYN, MANHATTAN, STATEN_ISLAND, and QUEENS in a given iteration.
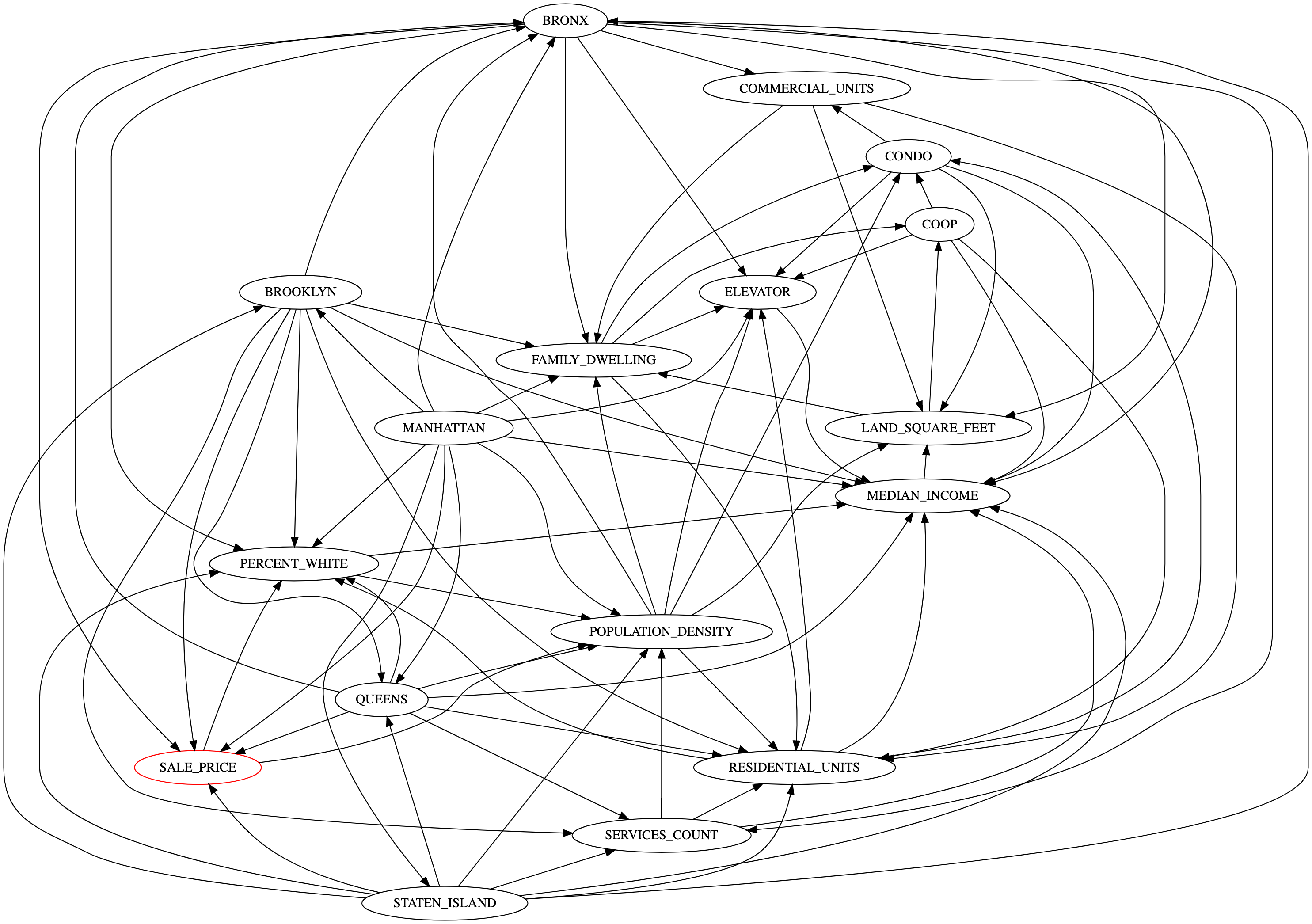
Figure 1
Given this graph, the parents and children of the SALE_PRICE– with the exception of the treatment variable being tested– will be used as the backdoor adjustment set for each of the treatment variables. This means that four of the boroughs will be included in the backdoor adjustment set, alongside PERCENT_WHITE and POPULATION_DENSITY Furthermore, the data yielding from the backdoor adjustment processes featured in backdoor.py, is presented in Figure 4.
Figure 2
| Treatment | Average Causal Effect | Confidence Interval |
|---|---|---|
| BROOKLYN | -1759368.766 | (-2204619.097, -1350677.114) |
| STATEN_ISLAND | -3242318.034 | (-3849001.805, -2750577.017) |
| BRONX | -2124969.992 | (-2517757.840, -1777306.324) |
| QUEENS | -2376241.155 | (-2856924.173, -1857450.184) |
| MANHATTAN | 12704278.334 | (10508549.500, 15480349.762) |
Discussion and Conclusion
The graph found from the Greedy Equivalence Search (Figure 1) did not feature edges between all of the treatment variables, which was expected, given that I didn’t allow for Tetrad to create unnecessarily complex graphs; while there was a relationship established in the DAG between all of the treatment variables, they are all directed edges. Such edges would make more sense if they were bidirected, considering that they are most certainly fully connected in both directions. However, as a result, the backdoor adjustment approach would have ended up inappropriate and would require changing.
Regarding the average causal effect, the data is presented in Figure 4 and appears to present that all of the boroughs, especially when compared to Manhattan, yield negative affects to the sales price. This is even consistent regarding the confidence intervals. Furthermore, it appears that the borough with the lowest value is Staten Island, with Queens and Bronx in close competition due to their overlapping confidence intervals, then Brooklyn and Manhattan.
Dealing with Linearity
In my introduction, I mention that I assume linear relationships between all of the variables: this may be, in reality, inaccurate. The most notable example of this may be the connection between residential units: while a single apartment may be in high demand, a property that contains two residential units may be less desirable, resulting in a lower price. However, purchasing a whole building is efficient and more valuable, meaning that then purchasing more residential units is more valuable. There is no variable that accounts for that in my data.
In order to somewhat deal with this linearity assumption, a machine learning version of the backdoor adjustment formula was written up, which used RandomForestRegressor in order to explore multiple possibilities regarding the likelihood of treatment variables being set to particular parameters. In backdoor.py, a function backdoor_ML is featured and then used to calculate the following ML based average causal affect. The results are featured in Figure 3.
Figure 3
| Treatment | Average Causal Effect | Confidence Interval |
|---|---|---|
| BROOKLYN | 443004.316 | (11381.310, 1271096.375) |
| STATEN_ISLAND | -342082.386 | (-540805.409, -45889.266) |
| BRONX | 58722.958 | (-40573.154, 547565.306) |
| QUEENS | 13004.852 | (-154845.842, 289796.614) |
| MANHATTAN | 16316418.597 | (10369625.148, 25390966.669) |
The table reveals that when the relationships between my included variables aren’t assumed to be linear, Staten Island becomes the remaining borough that has a negative causal effect; however, given the confidence intervals that include 0, that being the intervals for Bronx and Queens, it is possible that in reality, there is no benefit of being able to say that a property is located in either of these two locations. And still, it appears that properties in Brooklyn and Manhattan have objective value, just due to the name, with Manhattan beating out Brooklyn by a rather large margin.
Sensitivity Testing
This paper assumes that there directly exists an edge between the borough and the sale price. In order to ensure that this is actually true, I ran the FCIT test on the specific edges between the boroughs and the sale prices. This yielded the following results:
BROOKLYN HAS A FCIT RESULT OF 0.48312355531146034
MANHATTAN HAS A FCIT RESULT OF 0.9994838489001261
STATEN_ISLAND HAS A FCIT RESULT OF 0.0563579538762069
BRONX HAS A FCIT RESULT OF 0.5724756688589954
QUEENS HAS A FCIT RESULT OF 0.5649545577569158
Given my alpha value of 0.05, it appears that the only edge that could possibly exist between a borough and a sale price is the edge between Staten Island and the sale price– this makes sense given the persistently negative average causal affect identified by both backdoor adjustment and the ML backdoor adjustment approach. What is also of note is the very high result from the FCIT test regarding Manhattan: at nearly a value of 1, Manhattan value must be quantified by more than just the population density, median income, and similar features, such that the label of the name must not mean much at all when it comes to purchasing real estate properties.
However, these results can also be accounted for due to the linear approach of the FGES algorithm used to make the graph earlier in the paper– given additional computational complexity, I suppose only Staten Island is the place that truly, actively sucks.
References
U.S. Census Bureau. American community survey: S1901 income in the past 12 months (in 2020 inflation-adjusted dollars), a. URL https://data.census.gov/cedsci/table?q=income&g=1600000US3651000%248600000&y=2020&tid=ACSST5Y2020.S1901. [Online; Accessed 05.09.2021].
U.S. Census Bureau. American community survey: B02001 race, 2020, b. URL https://data.census.gov/cedsci/table?q=race&g=1600000US3651000%248600000&y=2020&tid=ACSDT5Y2020.B02001&tp=false. [Online; Accessed 05.09.2021].
Krzysztof Chalupka, Pietro Perona, and Frederick Eberhardt. Fast conditional independence test for vector variables with large sample sizes, 2018. URL https://arxiv.org/abs/1804.02747.
David Maxwell Chickering. Optimal structure identification with greedy search. Journal of Machine Learning Research, 3:507–554, 2002. data.BetaNYC. New york city neighborhoods populations and density. URL https://data.beta.nyc/en/dataset/pediacities-nyc-neighborhoods/resource/7caac650-d082-4aea-9f9b-3681d568e8a5. [Online; Accessed 05.09.2021].
NYC Department of Finance. New york city sales data from may 2021 - april 2022. URL https://www1.nyc.gov/site/finance/taxes/property-rolling-sales-data. [Online; Accessed 05.09.2021].
Judea Pearl. Causality. Cambridge University Press, 2009.
Joseph Ramsey, Madelyn Glymour, Ruben Sanchez-Romero, and Clark Glymour. A million variables and more: the fast greedy equivalence search algorithm for learning high-dimensional graphical causal models, with an application to functional magnetic resonance images. International Journal of Data Science and Analytics, 3(2):121–129, 2017.
Wikipedia contributors. List of new york city subway stations, 2022. URL https://en.wikipedia.org/wiki/List_of_New_York_City_Subway_stations. [Online; Accessed 05.09.2021].